cmepy.recorder

The cmepy.recorder computes and stores derived statistics from the solutions of the Chemical Master Equation (CME) produced by the cmepy.solver module.

Overview & Basic Usage

The general scheme for using a recorder consists of three steps:

1. Initialise a recorder r and define the random variables of interest using cmepy.recorder.create().
2. Repeatedly write CME solution data p to the recorder, along with the solution time t, via r.write(t, p).
3. Access derived statistics computed by the recorder.

To initialise a recorder, call cmepy.recorder.create(), passing one or more targets as arguments. Each target describes a group of random variables, and has the value (names, transforms), a pair of lists. The i-th random variable has the name names[i], and the states for this random variable are computed from states in the state space via the function transforms[i].

Note

The transforms argument is in fact optional. If left unspecified, the default value of transforms is a sequence of d coordinate projections, where d = len(names):

transforms = (lambda *x : x[0], ..., lambda *x : x[d-1])

These default transform functions describe the random variables of the coordinates of the state space.

For example, suppose states in the state space are pairs (a, b), where a and b are the species counts of the species 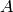and 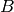. Then we define a recorder r with two random variables 'A' and 'B' for the corresponding species counts as follows:

r = cmepy.recorder.create(
    (['A', 'B'], [lambda *x : x[0], lambda *x : x[1]])
)

Alternatively, in this case we could omit the second item [lambda *x : x[0], lambda *x : x[1]] of the pair and equivaliently make use the default value of transforms, as described in the note above.

Chemical Master Equation (CME) solution data p is written to the recorder r by r.write(t, p), where t is the solution time.

To obtain the current solution p from a solver s, use p, p_sink = s.y. This assumes that the solver was initialised with the sink = True flag set. Conversely, if sink = False is set, the solution p may be obtained directly, by p = s.y. For more information regarding the CME solver and the sink flag, see the documentation for cmepy.solver.

Each CME solution p is represented as a Python dictionary, which maps states in the state space to the corresponding probabilities. This dictionary based scheme naturally lends itself to a sparse format, so states with zero probability may be omitted from the dictionary.

The recorder r creates a measurement instance for each random variable, which contains the corresponding marginal distributions and statistics. This data is computed using the times and data specified by the r.write(t, p) calls. For example, to access a list of expected values for the random variable 'A', use r['A'].expected_value. The i-th expected value in the list is computed from the solution p passed to the i-th call to the recorder’s r.write(t, p) method.

Measurement instances

To access a recorder r‘s measurement instances, use:

measurement = r[key]

Here, key must be one of the two following values:

1. the name of a random variable defined when r was created. In this case, measurement will contain the data for the marginal distribution of the random variable named key.
2. a tuple of names of random variables that were defined when r was created. In this case, measurement will contain the data for the joint distribution of the random variables in key.

For example, if random variables named 'X', 'Y' and 'Z' were defined when the recorder r was created, then the measurement instance for the joint distribution of 'Z' and 'X' may be accessed by:

measurement = r[('Z', 'X')]

Each measurement instance contains two main attributes: measurement.times and measurement.distributions. The former is a list of the times passed to r.write(t, p), while the latter is a list of the probability distributions for the random variable(s) specified by key at those times.

Other attributes defined by the measurement instance are lists of statistics derived from the distributions:

• measurement.expected_value : list of the expected values.
• measurement.expectation : synonymous with measurement.expected_value.
• measurement.variance : list of the variances. Only defined when measurement contains one-dimensional distributions.
• measurement.standard_deviation : list of the standard deviations. Only defined when measurement contains one-dimensional distributions.
• measurement.covariance : list of the covariances. Only defined when measurement contains two-dimensional distributions.