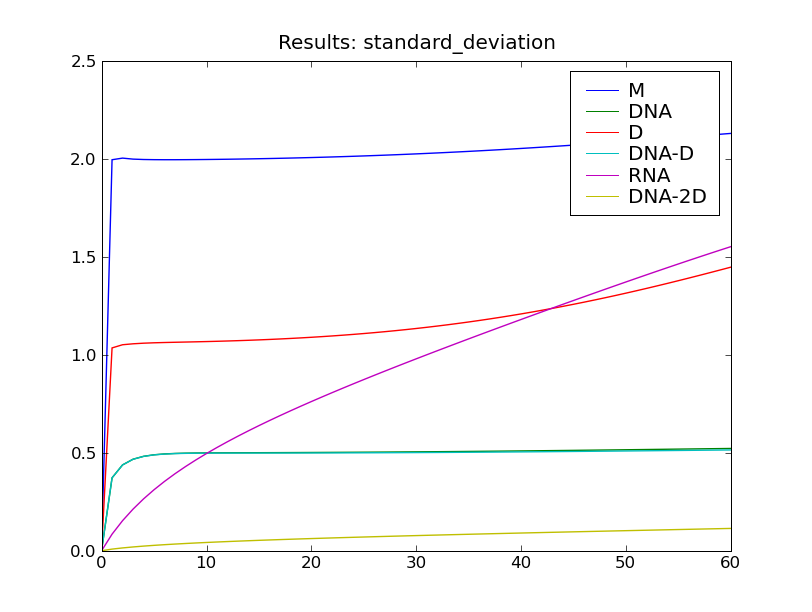
transcription_regulation : time dependent transcription regulation

Overview

The module cmepy.models.transcription_regulation defines a model of the transcription regulation system. This transcription regulation system was formulated by Goutsias [GOU05], and consists of 10 reactions:

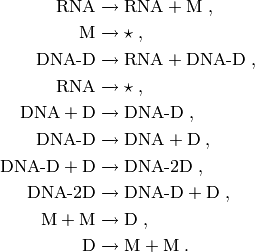
Initially, the system has 2 copies of DNA, 2 copies of M, and 6 copies of D.

The propensity functions of these reactions are all elementary. See the source code below or Goutsias [GOU05] for the rate coefficients. However, the three reactions

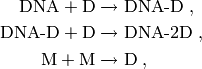
that is, those reactions in the system involving the combination of two different molecules, have their propensities scaled by a time dependent factor , where

Here, the constant 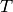is set to 35 minutes. See Goutsias [GOU05] for further details.

Running the model

To solve this model in CmePy and plot some results, simply open the Python interpreter and type:

>>> from cmepy.models import transcription_regulation
>>> transcription_regulation.main()

The model is solved from 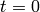to 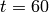using 60 equally-spaced time steps. The model is solved using a truncated state space, but the state space truncation error is still less than 1 percent of the total probability at the final time .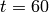

After solving the model, this script will display the the plots shown below.

Sample results

Source

"""
the transcription regulation example, as formulated by:

@article{goutsias2005quasiequilibrium,
  title={{Quasiequilibrium approximation of fast reaction
          kinetics in stochastic biochemical systems}},
  author={Goutsias, J.},
  journal={The Journal of chemical physics},
  volume={122},
  pages={184102},
  year={2005}
}

a time-independent approximation of this example was also considered by

@conference{burrage2006krylov,
  title={{A Krylov-based finite state projection algorithm for
          solving the chemical master equation arising in the
          discrete modelling of biological systems}},
  author={Burrage, K. and Hegland, M. and Macnamara, S. and Sidje, R.},
  booktitle={Proc. of The AA Markov 150th Anniversary Meeting},
  pages={21--37},
  year={2006}
}
"""

import numpy
import cmepy.model
from cmepy.util import non_neg

def create_time_dependencies():
    """
    returns time dependencies as dictionary of functions keyed
    by sets of reaction indices
    """  
    
    avogadro_number = 6.0221415e23
    cell_v_0 = 1.0e-15 # litres
    k = avogadro_number*cell_v_0
    cell_t = 35*60.0 # seconds
    
    def phi(t):
        return 1.0/(k*numpy.exp(numpy.log(2.0)*t/cell_t))
    
    return {frozenset([4, 6, 8]) : phi}

def create_model(dna_count=2, rna_max=15, m_max=15, d_max=15):
    
    # define mappings from state space to species copy counts
    dna =  lambda *x : x[0]
    dna_d = lambda *x : x[1]
    dna_2d = lambda *x : dna_count - x[0] - x[1]
    rna = lambda *x : x[2]
    m = lambda *x : x[3]
    d = lambda *x : x[4]
    
    # define reaction propensity constants
    k = (
        4.3e-2,
        7.0e-4,
        7.8e-2,
        3.9e-3,
        1.2e7,
        4.791e-1,
        1.2e5,
        8.765e-12,
        1.0e8,
        0.5,
    )
    
    return cmepy.model.create(
        name = 'Goutsias transcription regulation',
        species = (
            'DNA',
            'DNA-D',
            'DNA-2D',
            'RNA',
            'M',
            'D',
        ),
        species_counts = (
            dna,
            dna_d,
            dna_2d,
            rna,
            m,
            d,
        ),
        reactions = (
            'RNA -> RNA + M',
            'M -> *',
            'DNA-D -> RNA + DNA-D',
            'RNA -> *',
            'DNA + D -> DNA-D',
            'DNA-D -> DNA + D',
            'DNA-D + D -> DNA-2D',
            'DNA-2D -> DNA-D + D',
            'M + M -> D',
            'D -> M + M',
        ),
        propensities = (
            lambda *x : k[0] * rna(*x),
            lambda *x : k[1] * m(*x),
            lambda *x : k[2] * dna_d(*x),
            lambda *x : k[3] * rna(*x), 
            lambda *x : k[4] * dna(*x) * d(*x), 
            lambda *x : k[5] * dna_d(*x), 
            lambda *x : k[6] * dna_d(*x) * d(*x), 
            lambda *x : k[7] * dna_2d(*x), 
            lambda *x : k[8] * 0.5 * m(*x) * non_neg(m(*x) - 1), 
            lambda *x : k[9] * d(*x),
        ),
        transitions = (
            (0, 0, 0, 1, 0),
            (0, 0, 0, -1, 0),
            (0, 0, 1, 0, 0),
            (0, 0, 1, 0, 0),
            (-1, 1, 0, 0, -1),
            (1, -1, 0, 0, 1),
            (0, -1, 0, 0, -1),
            (0, 1, 0, 0, 1),
            (0, 0, 0, -2, 1),
            (0, 0, 0, 2, -1),
        ),
        shape = (dna_count+1, )*2 + (rna_max+1, m_max+1, d_max+1),
        initial_state = (dna_count, 0, 0, 2, 6)
    )

def main():
    """
    solves transcription regulation model and plot results
    """
    
    import cmepy.solver
    import cmepy.recorder
    
    m = create_model()
    
    solver = cmepy.solver.create(
        m,
        sink = True,
        time_dependencies = create_time_dependencies()
    )
    
    recorder = cmepy.recorder.create(
        (m.species,
         m.species_counts)
    )
    
    t_final = 60.0 
    time_steps = numpy.linspace(0.0, t_final, 61)
    for t in time_steps:
        solver.step(t)
        p, p_sink = solver.y
        print 't = %g; p_sink = %g' % (t, p_sink)
        recorder.write(t, p)
    
    cmepy.recorder.display_plots(
        recorder
    )

References

[GOU05]

(1, 2, 3) Goutsias, J., Quasiequilibrium approximation of fast reaction kinetics in stochastic biochemical systems, Journal of Chemical Physics (2005), Vol 122.