pap_pili : pap-pili epigenetic switch

Overview

The module cmepy.models.pap_pili defines a model of the pap-pili epigenetic switch system from Munksy and Khammash [MK06].

This system consists of 10 reactions:

The propensities of many of these reactions are non-elementary: the production of PapI is catalysed by LRP-DNA, while the propensities of the four reactions

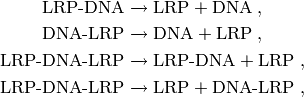
that is, the reactions where LRP unbinds from DNA, are all multiplied by the factor 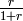, where denotes the copy count of the PapI species.

For the grim details of the reaction propensity functions and rate constants, either inspect the source code (see below) or refer to Munksy and Khammash [MK06].

Running the model

To solve this model in CmePy and plot some results, simply open the Python interpreter and type:

>>> from cmepy.models import pap_pili
>>> pap_pili.main()

This creates the pap-pili epigentic switch model with 5 initial copies of DNA, 5 initial copies of PapI, 100 initial copies of LRP, and zero initial copies of all other species. The model is solved from 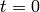to 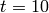using 100 equally-spaced time steps.

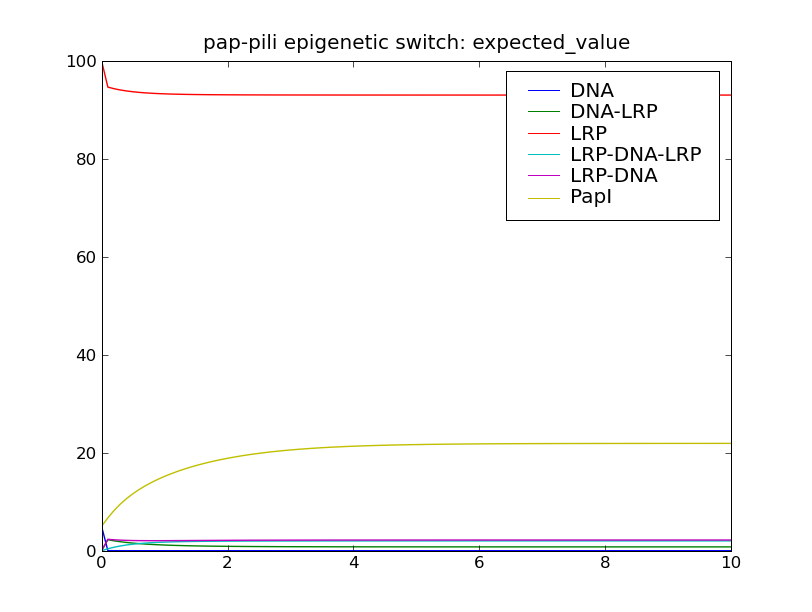
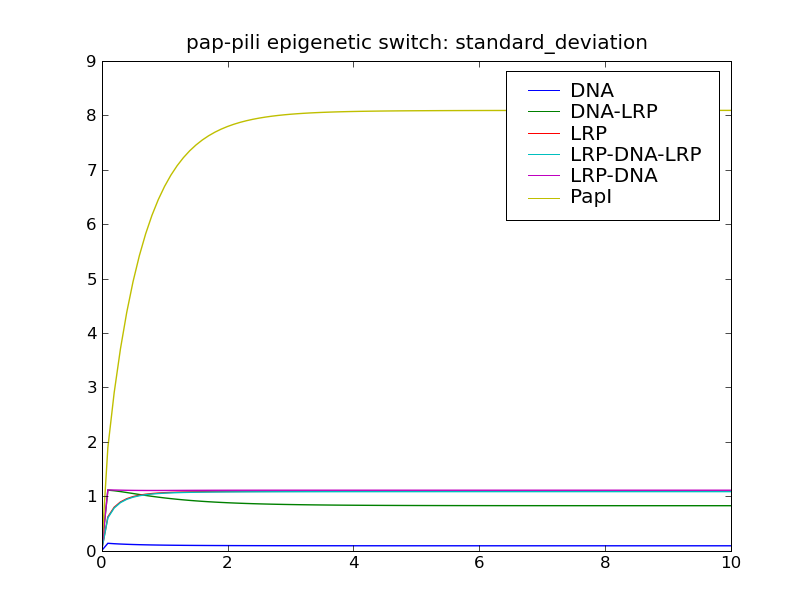
After solving the model, this script will display the following plots:

Sample results

Source

"""
Example implementation of the pap-pili epigenetic switch model.

This is the second example from Munsky & Khammash :

    @article{munsky2006finite,
      title={{The finite state projection algorithm for the
              solution of the chemical master equation}},
      author={Munsky, B. and Khammash, M.},
      journal={The Journal of chemical physics},
      volume={124},
      pages={044104},
      year={2006}
    }
"""

import cmepy.model
from cmepy.util import non_neg

def gen_states(max_papi = 100, dna_count = 1):
    """
    generates reachable states for pap-pili epigenetic switch model.
    """
    

    for dna in xrange(dna_count + 1):
        for dna_lrp in xrange(dna_count - dna + 1):
            for lrp_dna in xrange(dna_count - dna - dna_lrp + 1):
                for papi in xrange(max_papi + 1):
                    yield (dna, dna_lrp, lrp_dna, papi) 
    return

def create_model(max_papi = 100,
                 papi_count = 5,
                 dna_count = 1,
                 lrp_count = 100):
    """
    creates pap-pili epigenetic switch model.
    """
    
    # define mappings from state space to species counts
    dna = lambda *x : x[0]
    dna_lrp = lambda *x : x[1]
    lrp_dna = lambda *x : x[2]
    lrp_dna_lrp = lambda *x : non_neg(dna_count - x[0] - x[1] - x[2])
    lrp = lambda *x :non_neg(
        lrp_count - 2*lrp_dna_lrp(*x) - dna_lrp(*x) - lrp_dna(*x)
    )
    papi = lambda *x : x[3]
    
    def f(r):
        return r / (1.0 + r)
    
    # define reaction propensities
    props = (
        lambda *x : 1.0 * dna(*x) * lrp(*x),
        lambda *x : (2.5 - 2.25*f(papi(*x))) * lrp_dna(*x),
        lambda *x : 1.0 * dna(*x) * lrp(*x),
        lambda *x : (1.2 - 0.20 * f(papi(*x))) * dna_lrp(*x),
        lambda *x : 0.01 * lrp_dna(*x) * lrp(*x),
        lambda *x : (1.2 - 0.20 * f(papi(*x))) * lrp_dna_lrp(*x),
        lambda *x : 0.01 * dna_lrp(*x) * lrp(*x),
        lambda *x : (2.5 - 2.25 * f(papi(*x))) * lrp_dna_lrp(*x),
        lambda *x : 10.0 * lrp_dna(*x),
        lambda *x : 1.0 * papi(*x),
    )
    # define corresponding reaction state space offsets
    transitions = (
        (-1, 0, 1, 0), # LRP + DNA -> LRP-DNA
        (1, 0, -1, 0), # LRP-DNA -> LRP + DNA
        (-1, 1, 0, 0), # DNA + LRP -> DNA-LRP
        (1, -1, 0, 0), # DNA-LRP -> DNA + LRP
        (0, 0, -1, 0), # LRP-DNA + LRP -> LRP-DNA-LRP
        (0, 0, 1, 0), # LRP-DNA-LRP -> LRP-DNA + LRP
        (0, -1, 0, 0), # LRP + DNA-LRP -> LRP-DNA-LRP
        (0, 1, 0, 0), # LRP-DNA-LRP -> LRP + DNA-LRP
        (0, 0, 0, 1), # * -> PapI
        (0, 0, 0, -1), # PapI -> *
    )
    
    species_names = (
        'DNA',
        'DNA-LRP',
        'LRP-DNA',
        'LRP-DNA-LRP',
        'LRP',
        'PapI',
    )
    species_counts = (
        dna,
        dna_lrp,
        lrp_dna,
        lrp_dna_lrp,
        lrp,
        papi,
    )
    
    return cmepy.model.create(
        name = 'pap-pili epigenetic switch',
        species = species_names,
        species_counts = species_counts,
        propensities = props,
        transitions = transitions,
        shape = (dna_count+1, )*3 + (max_papi+1, ),
        initial_state = (dna_count, 0, 0, papi_count)
    )
    
def main():
    import numpy
    import cmepy.solver
    import cmepy.recorder
    import cmepy.domain
    
    dna_count = 5
    m = create_model(dna_count = dna_count)
    domain_states = cmepy.domain.from_iter(gen_states(dna_count = dna_count))
    solver = cmepy.solver.create(
        m,
        sink = True,
        domain_states = domain_states
    )
    recorder = cmepy.recorder.create(
        (m.species,
         m.species_counts)
    )
    
    time_steps = numpy.linspace(0.0, 10.0, 101)
    for t in time_steps:
        solver.step(t)
        p, p_sink = solver.y
        print 't = %g; p_sink = %g' % (t, p_sink)
        recorder.write(t, p)
    
    cmepy.recorder.display_plots(recorder, title = m.name)

References

[MK06]

(1, 2) Munsky, B. and Khammash, M., The finite state projection algorithm for the solution of the chemical master equation, Journal of Chemical Physics (2006), Vol 124.