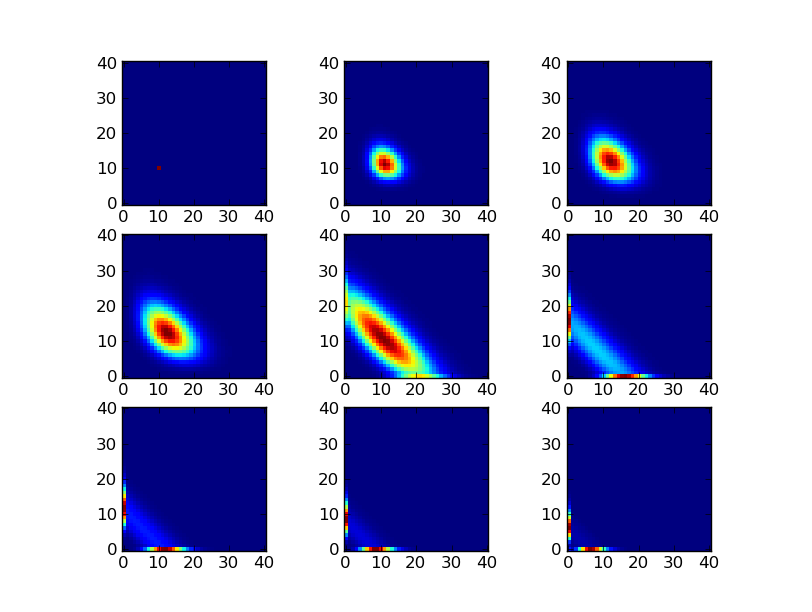
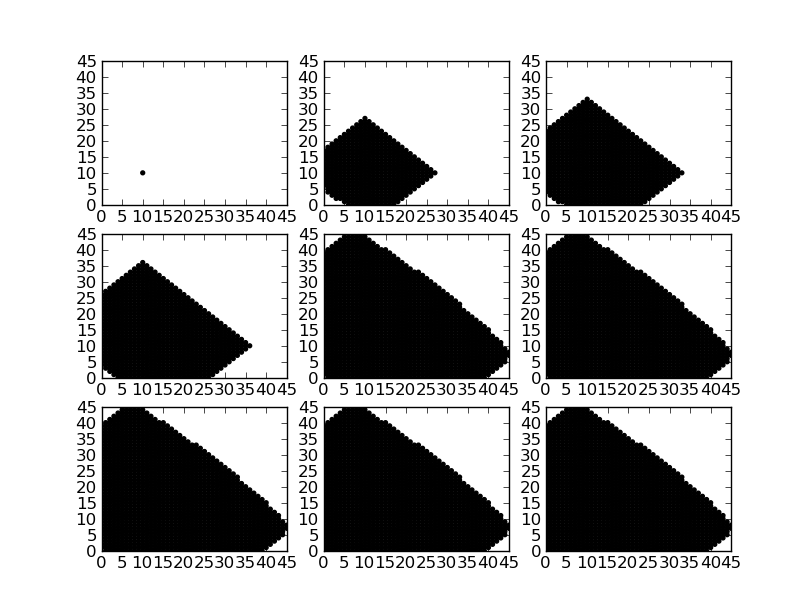
FSP example 2 : support expansion

Overview

This example demonstrates an FSP solver with a more complicated expansion strategy. Instead of expanding the entire domain, this expansion strategy expands states about the support of the solution. The solution is slightly compressed before computing its support in order to trim states with very low probability where possible. The states expanded about the support are then added to the domain of the FSP solver.

This expansion strategy requires more computation but leads to smaller domains. Smaller domains become especially important for higher dimensional models.

This support expansion strategy is implemented by the module cmepy.fsp.support_expander as follows:

"""
A solution-support based domain expansion routine for the FSP algorithm.
"""

import cmepy.domain
import cmepy.fsp.util
import cmepy.lexarrayset

class SupportExpander(object):
    """
    An FSP expander that expands states around the solution support.
    
    The domain is expanded to include all states reachable using the
    given transitions, up to the given depth, from the states that
    are contained in the support of a compressed epsilon approximation
    of the current solution.
    """
    def __init__(self, transitions, depth, epsilon):
        """
        An FSP expander that expands states around the solution support.
        
        The domain is expanded to include all states reachable using the
        given transitions, up to the given depth, from the states that
        are contained in the support of a compressed epsilon approximation
        of the current solution.
        """
        self.transitions = transitions
        self.depth = depth
        self.epsilon = epsilon
    
    def expand(self, **kwargs):
        """
        Returns expanded domain states
        """
        p = kwargs['p']
        support = cmepy.domain.from_iter(p.compress(self.epsilon))
        expanded_support = cmepy.fsp.util.grow_domain(
            support,
            self.transitions,
            self.depth
        )
        domain_states = kwargs['domain_states']
        return cmepy.lexarrayset.union(domain_states, expanded_support)

Output

Source

"""
example: uses Finite State Projection to solve the burr08 model
"""

from cmepy.models import burr08

import numpy
import cmepy.recorder
import cmepy.fsp.solver
import cmepy.fsp.support_expander
import cmepy.domain
import cmepy.statistics

# fsp_example_util a common plotting routine for the three fsp examples
import fsp_example_util

def main():
    """
    solve burr08 model using FSP with better expansion approach
    """
    
    # create model and initial states for domain
    model = burr08.create_model()
    initial_states = cmepy.domain.from_iter((model.initial_state, ))
    
    # Create expander for FSP expansion strategy.
    # The SolutionExpander only expands states around the
    # support of the current solution, instead of
    # expanding the entire domain
    expander = cmepy.fsp.support_expander.SupportExpander(
        model.transitions,
        depth = 1,
        epsilon = 1.0e-7
    )
    
    # create fsp solver for model, initial states, expander
    # - time dependencies for the burr08 model are also supplied
    fsp_solver = cmepy.fsp.solver.create(
        model,
        initial_states,
        expander,
        time_dependencies = burr08.create_time_dependencies()
    )
    
    # define time steps:
    # this problem is initially stiff so
    # we begin with some finer time steps
    # before changing to coarser steps
    time_steps = numpy.concatenate((
        numpy.linspace(0.0, 1.0, 10),
        numpy.linspace(2.0, 16.0, 15)
    ))
    
    # we want the error of the solution at the
    # final time to be bounded by epsilon
    epsilon = 1.0e-2
    num_steps = numpy.size(time_steps)
    # define how much error is tolerated per step
    max_error_per_step = epsilon / num_steps
    
    # create recorder to record species counts
    recorder = cmepy.recorder.create(
        (model.species, model.species_counts)
    )
    
    domains = []
    
    for i, t in enumerate(time_steps):        
        print 'STEP t = %g' % t
        fsp_solver.step(t, max_error_per_step)
        if i % 3 == 0:
            print 'recording solution and domain'
            # record the solution
            p, _ = fsp_solver.y
            recorder.write(t, p)
            # store a copy of the domain so we can plot it later
            domains.append(numpy.array(fsp_solver.domain_states))
    print 'OK'
    
    print 'plotting solution and domain'    
    fsp_example_util.plot_solution_and_domain(
        recorder[('A', 'B')],
        domains
    )

if __name__ == '__main__':
    main()