FSP example 1 : simple expansion

Overview

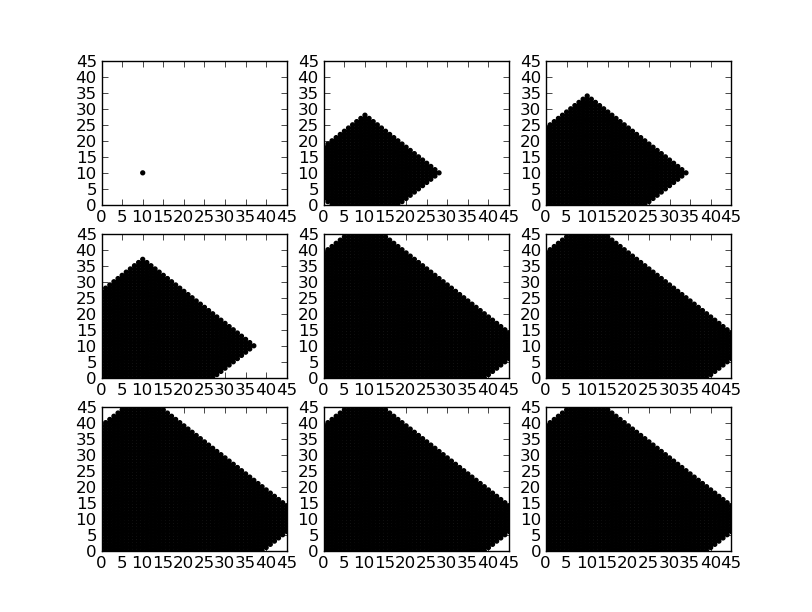
This example demonstrates an FSP solver with a very simple expansion strategy. In order to expand the domain, the domain is simply grown by adding all states reachable by making a sequence of state transitions, up to some maximum depth. This simple strategy leads to very large state spaces, but it works fine for the burr08 model, as it is a two-dimensional model with a limited number of states.

This simple expansion strategy is implemented by the module cmepy.fsp.simple_expander as follows:

"""
A simple domain expansion routine for the FSP algorithm.
"""

import cmepy.fsp.util

class SimpleExpander(object):
    """
    Simple FSP expander that expands the entire domain.
    
    The domain is expanded along the given transitions, up to the specified
    depth.
    """
    def __init__(self, transitions, depth):
        """
        Simple FSP expander that expands the entire domain.
    
        The domain is expanded along the given transitions, up to the specified
        depth.
        """
        self.transitions = transitions
        self.depth = depth
    
    def expand(self, **kwargs):
        """
        Returns expanded domain states
        """
        return cmepy.fsp.util.grow_domain(
            kwargs['domain_states'],
            self.transitions,
            self.depth
        )

Output

Source

"""
example: uses Finite State Projection to solve the burr08 model
"""

from cmepy.models import burr08

import numpy
import cmepy.recorder
import cmepy.fsp.solver
import cmepy.fsp.simple_expander
import cmepy.domain
import cmepy.statistics

# fsp_example_util a common plotting routine for the three fsp examples
import fsp_example_util

def main():
    """
    solve burr08 model using FSP with simple expansion approach
    """
    
    # create model and initial states for domain
    model = burr08.create_model()
    initial_states = cmepy.domain.from_iter((model.initial_state, ))
    
    # create simple expander for FSP expansion strategy
    # - this expands the ENTIRE domain by 3, along the
    #   state transitions
    expander = cmepy.fsp.simple_expander.SimpleExpander(
        model.transitions,
        depth = 3,
    )
    
    # create fsp solver for model, initial states, expander
    # - time dependencies for the burr08 model are also supplied
    fsp_solver = cmepy.fsp.solver.create(
        model,
        initial_states,
        expander,
        time_dependencies = burr08.create_time_dependencies()
    )
    
    # define time steps:
    # this problem is initially stiff so
    # we begin with some finer time steps
    # before changing to coarser steps
    time_steps = numpy.concatenate((
        numpy.linspace(0.0, 1.0, 10),
        numpy.linspace(2.0, 16.0, 15)
    ))
    
    # we want the error of the solution at the
    # final time to be bounded by epsilon
    epsilon = 1.0e-2
    num_steps = numpy.size(time_steps)
    # define how much error is tolerated per step
    max_error_per_step = epsilon / num_steps
    
    # create recorder to record species counts
    recorder = cmepy.recorder.create(
        (model.species, model.species_counts)
    )
    
    domains = []
    
    for i, t in enumerate(time_steps):
        print 'STEP t = %g' % t
        fsp_solver.step(t, max_error_per_step)
        if i % 3 == 0:
            print 'recording solution and domain'
            # record the solution
            p, _ = fsp_solver.y
            recorder.write(t, p)
            # store a copy of the domain so we can plot it later
            domains.append(numpy.array(fsp_solver.domain_states))
    print 'OK'
    
    print 'plotting solution and domain'    
    fsp_example_util.plot_solution_and_domain(
        recorder[('A', 'B')],
        domains
    )

if __name__ == '__main__':
    main()