Sparse state spaces

The cmepy.solver.create() function accepts the optional keyword argument domain_states. By default, if no domain_states argument is given, CmePy generates a dense ‘rectangular’ state space with dimensions specified by m.shape, where m is the value of the model argument passed to cmepy.solver.create().

However, often it is far more efficient to specify sparse state spaces. The cmepy.domain module provides a number of utility routines to ease the construction of sparse state spaces. The most important one is the from_iter() function:

cmepy.domain.from_iter(state_iter)

from_iter(state_iter) -> array

Returns array of all states from the state iterator ‘state_iter’.

Provided we have a suitable state_iter, we can create a solver using the sparse state space defined by state_iter as follows:

from cmepy import domain, model, solver

m = model.create(
    ... # model definition goes here
)

state_iter = ... # create state_iter somehow

s = solver.create(
    model = m,
    sink = True,
    domain_states = domain.from_iter(state_iter)
)

But what is a ‘state iterator’? A state iterator is simply any iterable object – such as a list, a set, a dictionary or a generator expression – that contains states. The states provided by the state iterator are assumed to be length- tuples of integers, for some fixed integer .

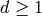Example: sparse state space for a mono-molecular system

For a concrete example, consider the following mono-molecular system of reactions:

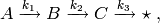
where 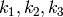are all positive constants, and the initial copy counts are 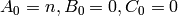, for some positive integer .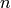

Note

Here, 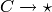is used to denote a ‘pure decay’ reaction. This reaction consumes the species 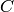and produces nothing, which is denoted . If this seems distasteful, another interpretation is to simply assume that the reaction in fact transforms 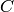into some product which we ignore.

Let’s consider a reaction count state space for this model. Let each state 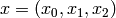be a triple of non-negative integers, where 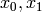and 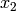denote the counts of the reactions 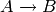, 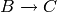and 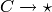respectively.

Since the third reaction may only occur following the second reaction, which in turn may only occur after the first reaction, which can occur up to 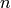times, the state space 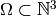is defined as:

We can define a generator in Python to yield precisely these states:

def gen_states(n):
    for x_0 in xrange(n + 1):
        for x_1 in xrange(x_0 + 1):
            for x_2 in xrange(x_1 + 1):
                yield (x_0, x_1, x_2)
    return

We call the generator with some chosen value for the initial copy count 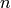of the species 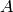, say 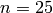, then pass the result as the domain_states keyword argument when creating the solver, after transformation via the function domain.from_iter():

s = solver.create(
    model = m,
    sink = True,
    domain_states = domain.from_iter(gen_states(25))
)

Example: sparse state space for Gardner’s gene toggle model

Consider the following system, consisting of the two imaginatively-named species 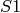and :

The initial copy counts are zero copies of both 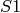and .

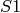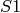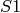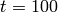This system is Munsky & Khammash’s formulation of Gardner’s gene toggle [GCC00], [MK08]. The two species and compete: copies of inhibit the production of , while conversely, copies of inhibit the production of . The solution of the chemical master equation for this system after seconds illustrates the result of these competetive dynamics:

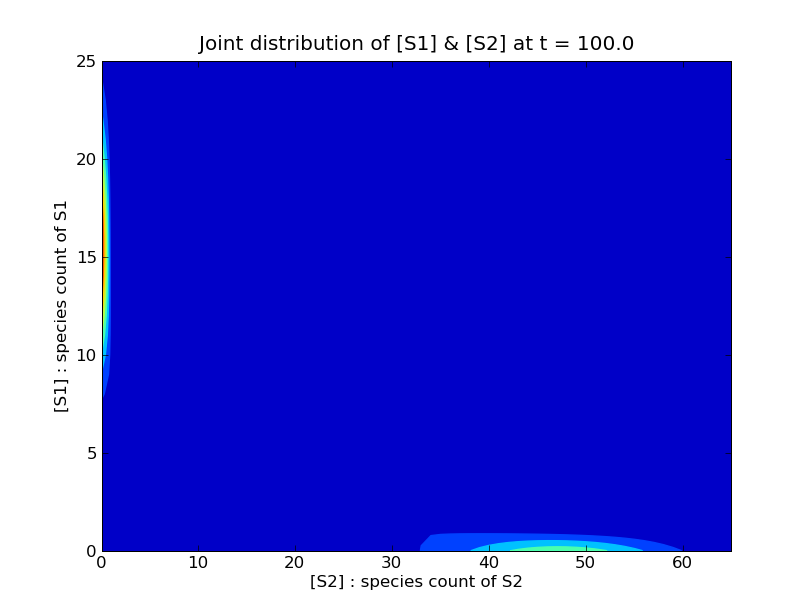
Since most of the probability is concentrated around the axes, we can still obtain a good approximation to the solution of the CME by only considering the states near each axis. We create a state space from the union of two rectangular regions about the axes as follows:

from cmepy import domain

r_a = (66, 6)
r_b = (10, 26)
states_a = set(domain.to_iter(domain.from_rect(r_a)))
states_b = set(domain.to_iter(domain.from_rect(r_b)))
states = domain.from_iter(states_a | states_b)

The function domain.from_rect() transforms the given shapes r_a and r_b to arrays containing all the states in the corresponding rectangular regions. We then contruct sets containing these states, using the function domain.to_iter() to create state iterators over the given state arrays. Finally, we union the two sets states_a and states_b via states_a | states_b, which is equivalent to states_a.union(states_b), then transform the resulting set to a state array by applying the function domain.from_iter().

References

[GCC00]

Gardner, T.S. and Cantor, C.R. and Collins, J.J., Construction of a genetic toggle switch in Escherichia coli, Nature (2000), volume 403, pp. 339 – 342.

[MK08]

Munsky, B. and Khammash, M., Computation of switch time distributions in stochastic gene regulatory networks, Proc. 2008 American Control Conference (June 2008), pp. 2761 – 2766.