dual_enzymatic : coupled enzymatic reactions

Overview

This model describes a system of coupled enzymatic reactions. The reactions composing this system are as follows:

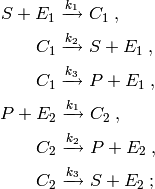
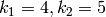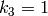The rate constants are and . The initial species counts are 50 copies of 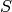, 20 copies 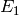of , and 10 copies of 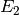. The other species counts are initially zero.

The first three reactions in the system describe an enzymatic reaction transforming the species 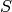into the spec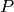ies . The second three reactions describe another enzymatic reaction transforming the species 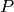back into .

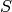Running the model

This model is defined by the module cmepy.model.dual_enzymatic. The source code for this model is listed below.

To try out this model, open the Python interpreter and enter:

>>> from cmepy.models import dual_enzymatic
>>> dual_enzymatic.main()

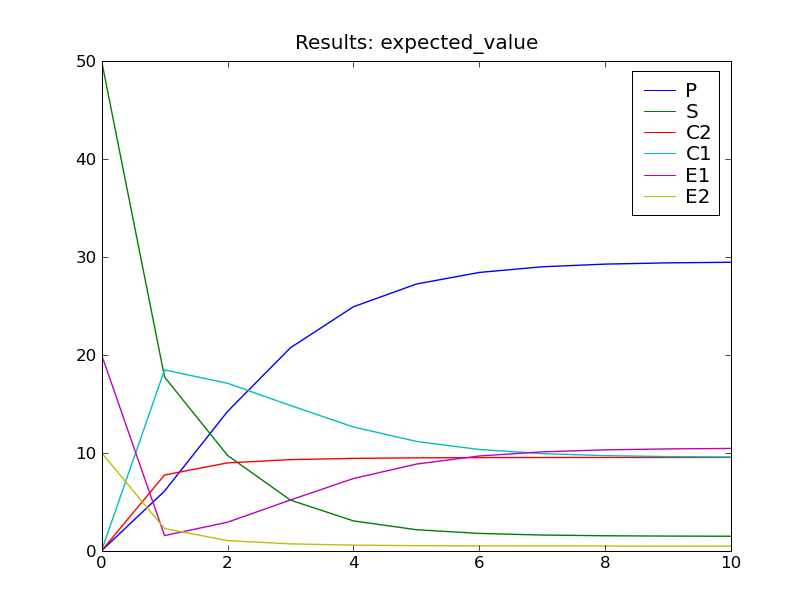
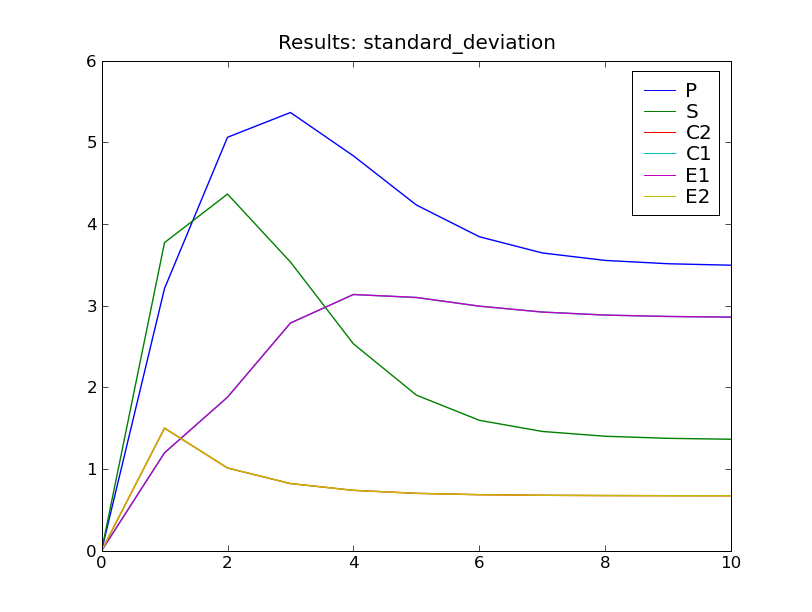
This will solve the system up to 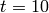, then display plots of the standard deviation and expected value of the species counts, as seen below.

Sample results

Source code

"""
Example system with two enzymatic reactions.

System :
    S + E1 <--> C1 --> P + E1
    P + E2 <--> C2 --> S + E2
"""

from cmepy import model

def default_initial_copies():
    """
    Returns default initial copies of species S, E1, E2 for the model.
    """
    return {
        'S' : 50,
        'E1' : 20,
        'E2' : 10,
    }
        

def gen_states(initial_copies = None):
    """
    Returns generator yielding all reachable states in state space.
    
    NB state space format: (c2_copies, c1_copies, s_copies)
    """
    
    if initial_copies is None:
        initial_copies = default_initial_copies()
    
    s_0 = initial_copies['S']
    e1_0 = initial_copies['E1']
    e2_0 = initial_copies['E2']
    for s in xrange(s_0+1):
        for c1 in xrange(min(e1_0, s_0 - s)+1):
            for c2 in xrange(min(e2_0, s_0 - s - c1)+1): 
                yield (c2, c1, s)
    return

def create_model(initial_copies = None):
    """
    Returns mapping storing model.
    
    NB state space format: (c2_copies, c1_copies, s_copies)
    """
    
    if initial_copies is None:
        initial_copies = default_initial_copies()
    
    s_copies = lambda *x : x[2]
    c1_copies = lambda *x : x[1]
    c2_copies = lambda *x : x[0]
    p_copies = lambda *x : initial_copies['S'] - x[0] - x[1] - x[2]
    e1_copies = lambda *x : initial_copies['E1'] - x[1]
    e2_copies = lambda *x : initial_copies['E2'] - x[0]
    
    return model.create(
        name = 'dual enzymatic reactions',
        reactions = (
            'S+E1 -> C1',
            'C1 -> S+E1',
            'C1 -> P+E1',
            'P+E2 -> C2',
            'C2 -> P+E2',
            'C2 -> S+E2',
        ),
        propensities = (
            lambda *x : 4.0*s_copies(*x)*e1_copies(*x),
            lambda *x : 5.0*c1_copies(*x),
            lambda *x : 1.0*c1_copies(*x),
            lambda *x : 4.0*p_copies(*x)*e2_copies(*x),
            lambda *x : 5.0*c2_copies(*x),
            lambda *x : 1.0*c2_copies(*x),
        ),
        transitions = (
            (0, 1, -1),
            (0, -1, 1),
            (0, -1, 0),
            (1, 0, 0),
            (-1, 0, 0),
            (-1, 0, 1),
        ),
        species = (
            'S',
            'C1',
            'C2',
            'P',
            'E1',
            'E2',
        ),
        species_counts = (
            s_copies,
            c1_copies,
            c2_copies,
            p_copies,
            e1_copies,
            e2_copies,
        ),
        initial_state = (0, 0, initial_copies['S'])
    )

def main():
    """
    Solve dual enzymatic reaction system
    """
    
    import numpy
    import cmepy.solver
    import cmepy.recorder
    import cmepy.domain
    
    model = create_model()
    
    solver = cmepy.solver.create(
        model = model,
        sink = True,
        domain_states = cmepy.domain.from_iter(gen_states()),
    )
    
    recorder = cmepy.recorder.create(
        (model.species, model.species_counts)
    )
    
    t_final = 10.0
    steps_per_time = 25
    time_steps = numpy.linspace(0.0, t_final, int(steps_per_time*t_final) + 1)
    
    print 'solving dual enzymatic system to t_final = %.2f' % t_final
    for step, t in enumerate(time_steps):
        print 't = %.2f' % t
        solver.step(t)
        # record results every second, not every step
        if step % steps_per_time == 0:
            print 'recording solution'
            p, p_sink = solver.y
            recorder.write(t, p)
    
    cmepy.recorder.display_plots(recorder)