Example: a single reaction

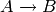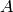Consider the reaction , where initially there are 20 copies of the species , and 0 copies of the species .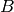

We will create a short CmePy script to solve the Chemical Master Equation for this reaction. Our script shall produce the following plot, which illustrates how the probability distribution over the reaction counts evolves in time:

Observe how the probability begins concentrated at reaction count zero for the time 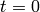, quickly diffuses, then begins to accumulate at reaction count 20, where all the copies of the species 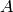have been exhausted.

Defining the model

A CmePy script typically contains three main components

1. A model, which defines the system of reactions.
2. A solver, which solves the Chemical Master Equation (CME) for the model.
3. A recorder, which stores solutions computed by the solver, and provides a simple interface for computing and plotting results, such as the expected value, standard deviation, or marginal distribution for species counts.

We begin by defining a model m for this simple system of reactions:

from cmepy import model

initial_copies = 20

m = model.create(
    propensities = [lambda x: initial_copies - x],
    transitions = [(1, )],
    shape = (initial_copies + 1, ),
    initial_state = (0, )
)

The reactions are specified by the propensities and transitions keyword arguments. Since there is only a single reaction 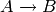in this example, only one propensity function and transition are required. The propensity function lambda x: initial_copies - x returns the propensity of the reaction in terms of the reaction count x, while the transition (1, ) specifies that the reaction increases the reaction count x by 1.

The argument shape is used to define the range of reaction counts that the solver will consider when solving the CME. Since initial_copies = 20, the range of reaction counts considered for shape = (initial_copies + 1, ) is .

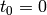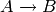Finally, the argument initial_state defines that the CME is initialised in the state (0, ). In other words, at the initial time , the probability that there have been zero occurrences of the reaction is 1.

Note

You may be wondering why shape, initial_state, and the item contained by transitions have tuple values, not scalar values. This is because models typically represent systems containing more than one reaction.

Solving the model

We now create a solver s to solve the CME for the model m:

import numpy
from cmepy import solver

s = solver.create(
    model = m,
    sink = False
)

time_steps = numpy.linspace(0.0, 3.0, 6)
for t in time_steps:
    s.step(t)

This code initialises the solver using solver.create and then advances the solution of the chemical master equation from time 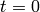to time 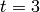using 5 uniformly spaced steps.

The attribute s.y stores the current solution of the CME computed by the solver. This solution is essentially a dictionary, mapping reaction counts to probabilities. For example, s.y[(3, )] is the probability that there have been exactly three occurances of the reaction.

Note

The keyword argument sink = False indicates that the state space of the model is not truncated, that is, there is no way probability may ‘leak’ out of the states under consideration of the solver.

Recording and plotting results

Now we add a recorder r to record the solutions and compute statistics:

from cmepy import recorder

r = recorder.create(
    (('A->B', ), )
)

time_steps = numpy.linspace(0.0, 3.0, 6)
for t in time_steps:
    s.step(t)
    r.write(t, s.y)

The call to recorder.create initialises a recorder with a single random variable named 'A->B'. By default, this random variable is the first coordinate of the state space, which in this case is the reaction count of the reaction .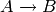

Solutions are written to the recorder by r.write(t, s.y), where t is the time of the solution, and s.y is the solution computed by the solver s.

The measurements recorded for the random variable named 'A->B' are stored inside r under the key 'A->B'. For example, the attribute r['A->B'].expected_value is a list of the expected values of the random variable 'A->B' that have been recorded by r.

We can now use the recorder r to generate the marginal distributions over the reaction counts, for each time step, and then plot these distributions using Matplotlib‘s pylab module:

import pylab

pylab.figure()

for t, d in zip(r['A->B'].times, r['A->B'].distributions):
    marginal = d.to_dense(m.shape)
    pylab.plot(marginal, label = 't = %.1f' % t)

pylab.xlabel('Reaction count')
pylab.ylabel('Probability')
pylab.legend()
pylab.savefig('simple_plot.png')

We access a measurement instance for the random variable 'A->B' via r['A->B']. This measurement instance contains the attributes times and distributions, which are the lists of measurement times and marginal distributions, respectively.

Each marginal distribution d is represented as a ‘sparse’ dictionary structure, which must be converted to a ‘dense’ flat array for plotting, using the method d.to_dense(shape). In this case, the shape of the array we want is the same shape of the model, m.shape.

Note

Python’s built-in zip(a, b) function takes two lists a and b, and returns the list [(a[0], b[0]), (a[1], b[1]), ...].

Note

You may like to experiment using pylab.show() instead of pylab.savefig('simple_plot.png').

Bringing everything together

Mixing all the above ingredients together yields the following Python script:

import numpy
import pylab
from cmepy import model, solver, recorder

def main():
    initial_copies = 20
    
    m = model.create(
        propensities = [lambda x: initial_copies - x],
        transitions = [(1, )],
        shape = (initial_copies + 1, ),
        initial_state = (0, )
    )
    
    s = solver.create(
        model = m,
        sink = False
    )
    
    r = recorder.create(
        (('A->B', ), )
    )
    
    time_steps = numpy.linspace(0.0, 3.0, 6)
    for t in time_steps:
        s.step(t)
        r.write(t, s.y)
    
    pylab.figure()
    for t, d in zip(r['A->B'].times, r['A->B'].distributions):
        marginal = d.to_dense(m.shape)
        pylab.plot(marginal, label = 't = %.1f' % t)
    pylab.xlabel('Reaction count')
    pylab.ylabel('Probability')
    pylab.legend()
    pylab.savefig('simple_plot.png')

if __name__ == '__main__':
    main()

Suppose this script is saved as simple.py. Then we can run the script from the command line via:

python simple.py

This will save a plot of the reaction count distributions to simple_plot.py.

Note

If Python complains with the message ImportError: No module named cmepy, check that CmePy has been installed.